RBTree的定义

  1. 任何一个节点都有颜色，黑色或者红色。
  2. 根节点是黑色的。
  3. 父子节点之间不能出现两个连续的红节点。
  4. 任何一个节点向下遍历到其子孙的叶子节点，所经过的黑节点个数必须相等。
  • 如果一个节点存在黑子节点，那么该节点肯定有两个子节点
  1. 空节点被认为是黑色的。
1
2
3
4
5
6
7
class  Node<T>{
   public   T value;
   public   Node<T> parent;
   public   boolean isRed;
   public   Node<T> left;
   public   Node<T> right;
}

红黑树在插入和删除操作时会维持树的平衡，即保证树的高度在[logN,logN+1]，查找、删除和插入操作复杂度是O(logN)。

旋转

旋转操作(Rotate)的目的是使节点颜色符合定义，让RBTree的高度达到平衡。

左旋：以某个节点作为支点(旋转节点)，其右子节点变为旋转节点的父节点，右子节点的左子节点变为旋转节点的右子节点，左子节点保持不变。

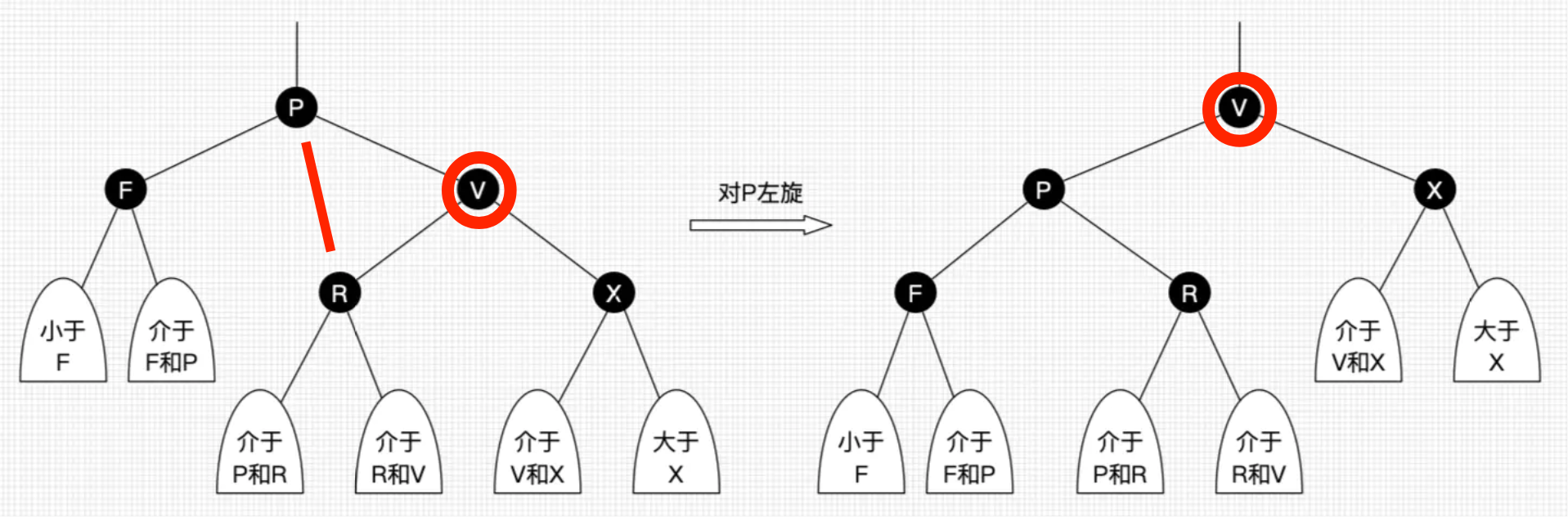
右旋：以某个节点作为支点(旋转节点)，其左子节点变为旋转节点的父节点，左子节点的右子节点变为旋转节点的左子节点，右子节点保持不变。

查找

值小于当前节点，查找左子树，值大于当前节点，查找右子树

插入

先查找插入位置（和查找一样），插入红色节点，再自平衡

核心思想是：解决两个连续红色节点问题。

策略：左旋、右旋、变色

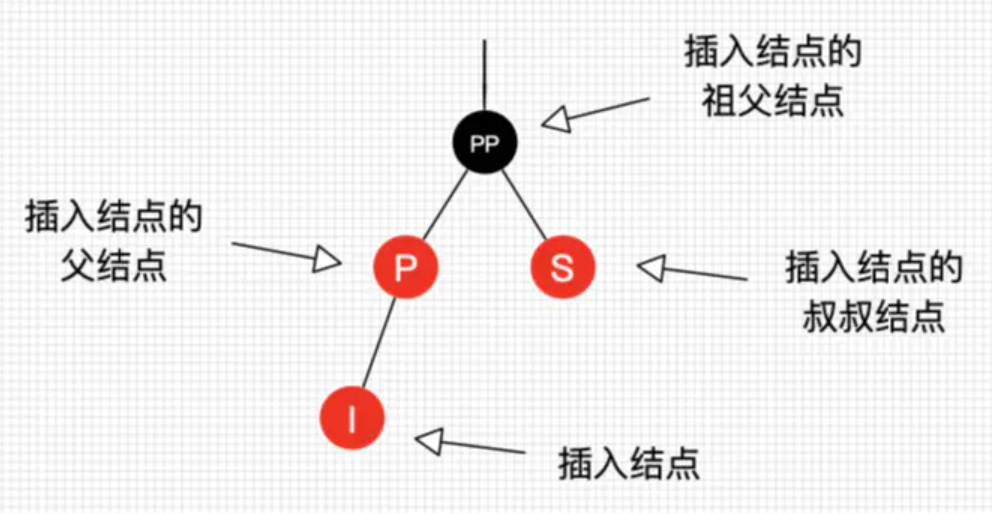
情境4：如果插入的父节点为红节点，那么该父节点不可能为根节点，所以插入节点总是存在祖父节点。这点很重要，因为后续的旋转操作肯定需要祖父节点的参与。

4.1：

如果PP的父节点是黑色，那么无需再做任何处理；但如果PP的父节点是红色，还需要把PP当作新的插入节点，继续做插入操作自平衡处理

如果PP是根节点，那么需要重新把PP设为黑色

唯一一种会增加红黑树黑色节点层数的插入情景

4.2.1

4.2.2

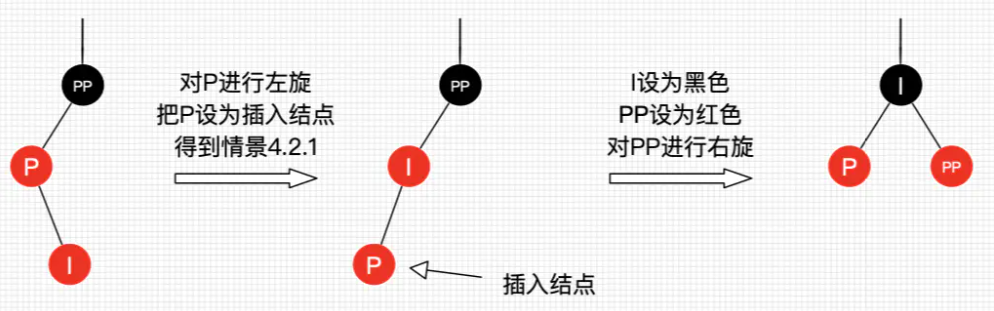
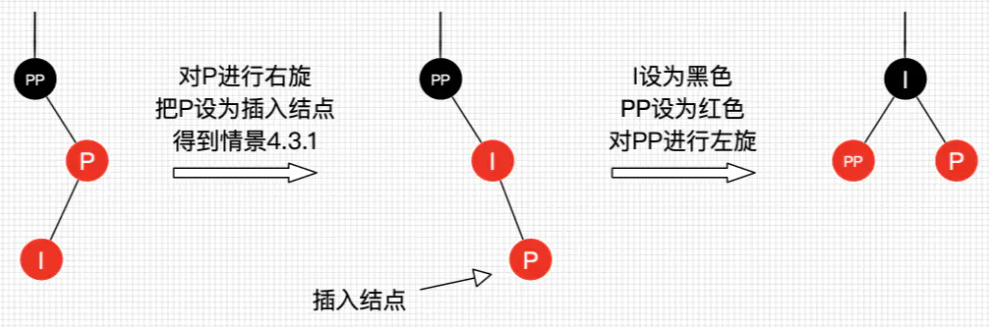
4.3.1

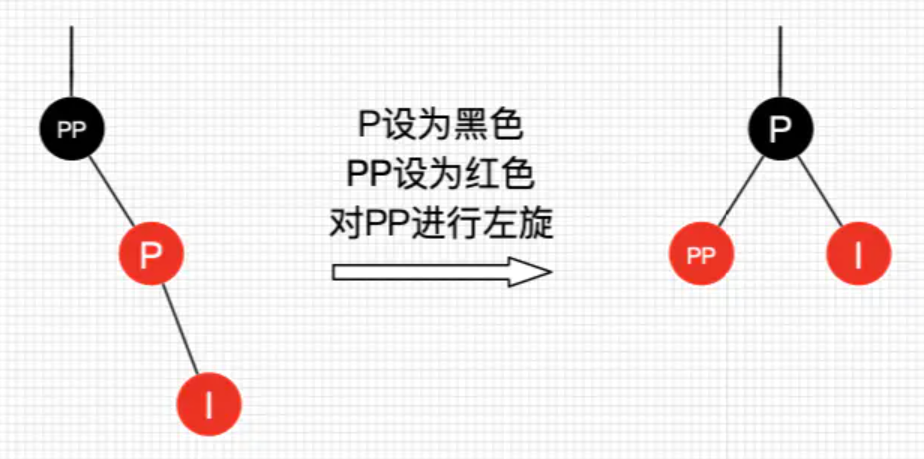
4.3.2

删除

删除操作会删除对应的节点

  • 叶子节点就直接删除

  • 非叶子节点，会用对应的中序遍历的后继节点来替换要删除节点的位置（删除节点的右子树中最左节点）

    • 替换节点是红色，直接替换，颜色改为和删除节点一致
    • 替换节点是黑色，进行修复

核心思想是：替代节点补位到删除位置后，怎么保证原来位置的树的黑色节点满足红黑树定义4（到叶子节点经过相同个数黑色节点）

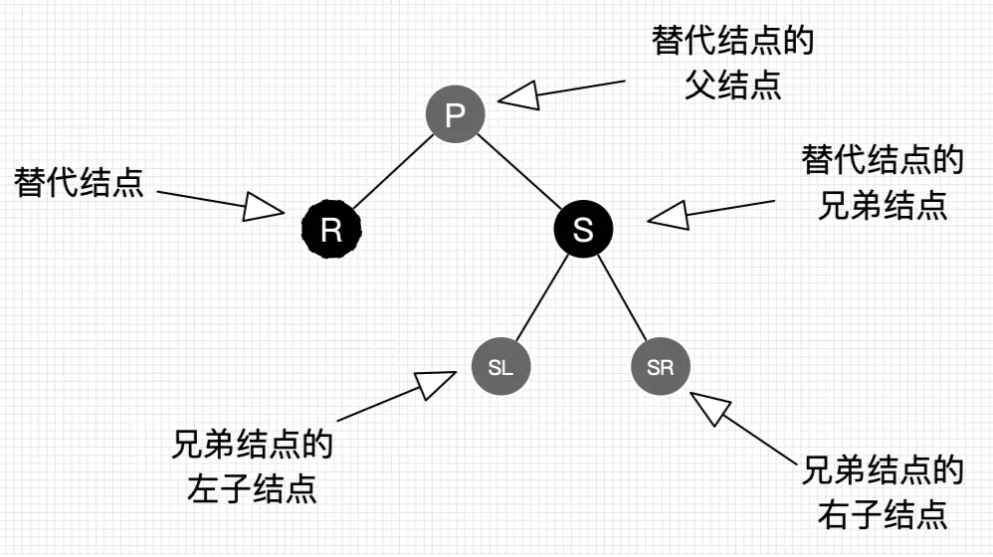
R是即将被替换到删除节点的位置的替代节点

以下均以替换节点是父节点的左子节点为例，镜像树相应改变即可

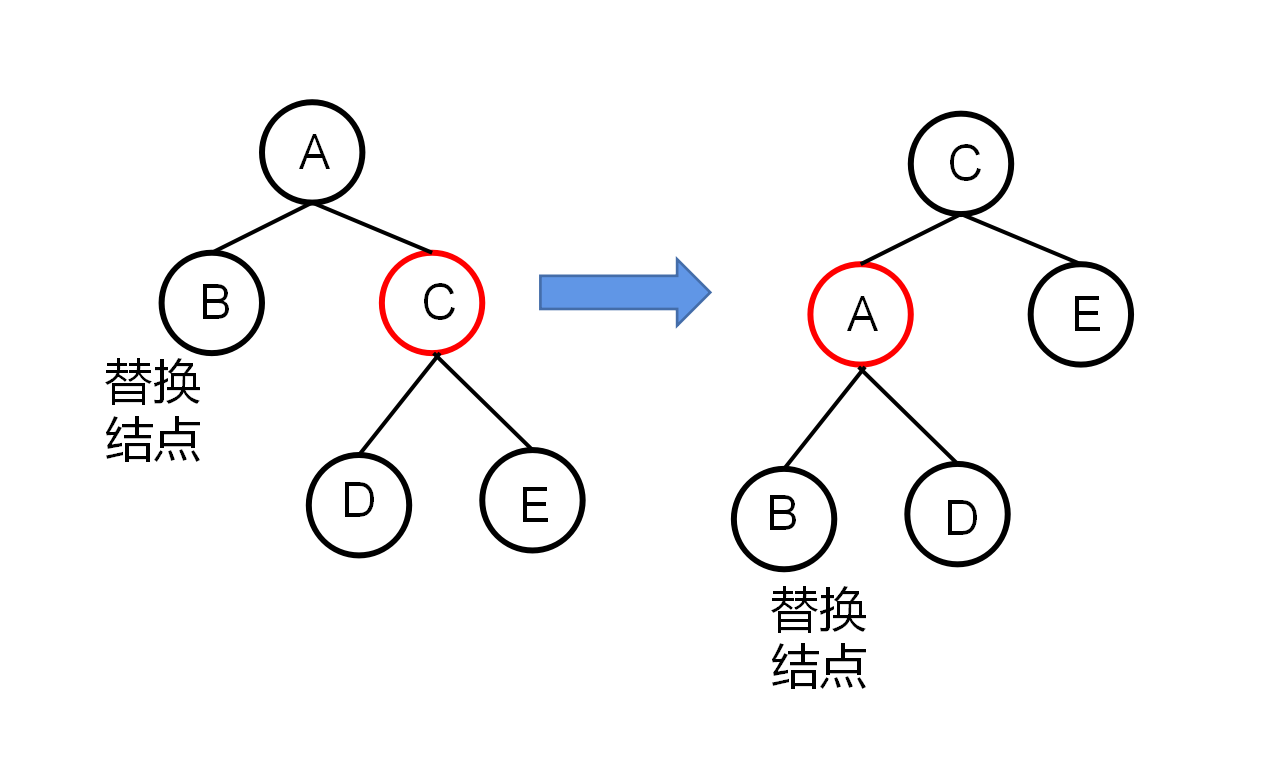
  1. 替换节点的兄弟节点是红色的节点。

    由于无法从兄弟节点借到一个黑节点来填补替换的黑节点，需要将兄弟节点提升到父节点

    兄弟节点变黑，父节点变红，再对父节点左旋，从而变成剩下三种case之一

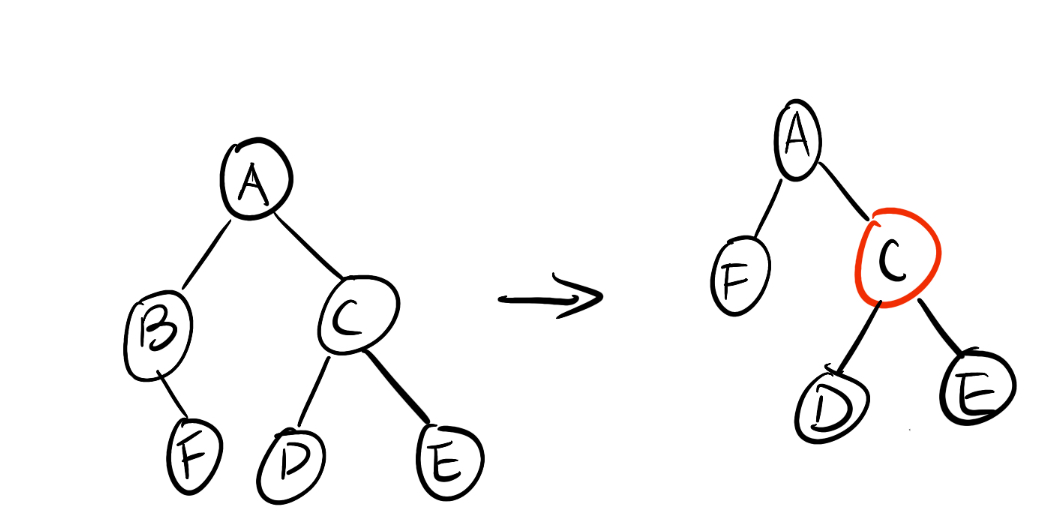
  2. 替换节点的兄弟节点是黑色的节点，且兄弟节点的子节点都是黑色的

    兄弟节点变红（可以保证树的局部的颜色符合定义）,父节点视为新的替换节点，继续向上回溯

  3. 替换节点的兄弟节点是黑色的节点，且兄弟节点的子节点左黑右红

    兄弟节点颜色变为父节点颜色，把父节点和兄弟节点的右子节点设为黑色，对父节点左旋

  4. 替换节点的兄弟节点是黑色的节点，且兄弟节点的子节点左红右黑

    兄弟节点改为红色，左孩子改为黑色，再对兄弟节点右旋，回到case3