动态规划

框架

确定状态：原问题和子问题中变化的变量。状态决定了问题什么时候算是解决了。
确定dp函数定义：
- 一般就是问题
- 也可以是中间子问题，比如第二、三个例题
确定选择并择优：对于当前状态，有哪些选择可以改变状态，向着问题的解决前进。
明确badcase
使用备忘录数组记录已经访问过的状态

例题

最长公共子序列

题目：#1143

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。例如，”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

思路：

用两个指针，从指针位置到字符串末尾，是当前状态下的字符串。状态量其实就是字符串长度。
dp函数：返回当前长度下的两个字符串的最长公共子序列长度
选择并择优：如果当前两个指针的字符相等，则返回递归函数值+1；如果不等，有三种可能：
- 指针1的字符在最长公共子序列中，指针2不在。则指针2往后移一位，递归调用dp函数
- 指针2的字符在最长公共子序列中，指针1不在。则指针1往后移一位，递归调用dp函数
- 指针1,2的字符都不在，其实包含在前两种情况内。
- 取返回值最大的那种选择。
badcase是任意一个指针到字符串末尾后了，则一个字符串变为空，返回0
最后使用备忘录数组记录已经计算过的情况值。

import java.util.*;
class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int [][] dptable=new int[text1.length()][text2.length()];
        for(int[] row:dptable){
            Arrays.fill(row,-1);
        }
        return dp(text1,0,text2,0,dptable); //1
    }
    public int dp(String s1,int idx1,String s2,int idx2,int[][]dptable){ //2
        if(idx1==s1.length()||idx2==s2.length())return 0; //4
        if(dptable[idx1][idx2]!=-1)return dptable[idx1][idx2]; //5
        if(s1.charAt(idx1)==s2.charAt(idx2)){ //3
            dptable[idx1][idx2]=1+dp(s1,idx1+1,s2,idx2+1,dptable);
        }
        else{
            dptable[idx1][idx2]=Math.max(
                dp(s1,idx1+1,s2,idx2,dptable),
                dp(s1,idx1,s2,idx2+1,dptable)
            );
        }
        return dptable[idx1][idx2];
    }
}

// java
class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length(), n = text2.length();
        int[][] dp = new int[m + 1][n + 1];

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 获取两个串字符
                char c1 = text1.charAt(i), c2 = text2.charAt(j);
                if (c1 == c2) {
                    // 去找它们前面各退一格的值加1即可
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                } else {
                    //要么是text1往前退一格，要么是text2往前退一格，两个的最大值
                    dp[i + 1][j + 1] = Math.max(dp[i + 1][j], dp[i][j + 1]);
                }
            }
        }
        return dp[m][n];
    }
}

数组中等差递增子区间的个数

题目：#413

数组 A 包含 N 个数，且索引从0开始。数组 A 的一个子数组划分为数组 (P, Q)，P 与 Q 是整数且满足 0<=P<Q<N 。如果满足以下条件，则称子数组(P, Q)为等差数组：元素 A[P], A[p + 1], …, A[Q - 1], A[Q] 是等差的。并且 P + 1 < Q 。函数要返回数组 A 中所有为等差数组的子数组个数。

这里的dp函数就是一个子问题: dp[i] 表示以 A[i] 为结尾的等差递增子区间的个数。最后求完以后只要取dp数组的最大值就可以解决原问题。

public int numberOfArithmeticSlices(int[] nums) {
    int n=nums.length;
    if(n<3)return 0;
    int[]dp=new int[n];

    for(int i=2;i<n;i++){
        if(nums[i]-nums[i-1]==nums[i-1]-nums[i-2]){
            dp[i]=dp[i-1]+1;
        }
    }
    int sum=0;
    for(int v:dp)sum+=v;
    return sum;   
}

最长递增子序列

题目：#300

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

dp[i]是以当前数结尾的最长递增子序列

public int lengthOfLIS(int[] nums) {
    int n=nums.length;
    if(n==0)return 0;
    int[]dp=new int[n];
    for(int i=0;i<n;i++){
        int maxnow=1;
        for(int j=0;j<i;j++){
            if(nums[j]<nums[i]){
                maxnow=Math.max(maxnow,dp[j]+1);
            }
        }
        dp[i]=maxnow;
    }
    Arrays.sort(dp);
    return dp[n-1];
}

滑动窗口

主要解决字符串子串匹配问题

框架

维护一个窗口，不断滑动，然后更新答案

int left = 0, right = 0;

while (right < s.size()) {
    // 增大窗口
    window.add(s[right]);
    right++;

    while (window needs shrink) {
        // 缩小窗口
        window.remove(s[left]);
        left++;
    }
}

一般用HashMap实现窗口，用到getOrDefault(key,defaultvalue)函数来获取值，同时避免key不存在时得到null。

例题

最小覆盖子串

题目：#76

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。注意：如果 s 中存在这样的子串，我们保证它是唯一的答案。

1 2	输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC"

import java.util.*;
class Solution {
    public String minWindow(String s, String t) {
        HashMap<Character,Integer> need=new HashMap<>();
        HashMap<Character,Integer> window=new HashMap<>();
        int start=0,end=0,len=s.length()+1;
        int fstart=0,fend=0;
        boolean flag=false,flag2=false;
        String re="";
        for(int i=0;i<t.length();i++){//need中记录t的每个字符出现次数
            need.put(t.charAt(i),need.getOrDefault(t.charAt(i),0)+1);
        }
        while(end<s.length()){
            flag=false;
            while(!flag2map(need,window)&&end<s.length()){//窗口右移，直到window包含所有t中字符
                window.put(s.charAt(end),window.getOrDefault(s.charAt(end),0)+1);
                end++;
            }
            while(flag2map(need,window)){//窗口左移，直到window中包含t中全部字符不成立
                if(need.containsKey(s.charAt(start))){
                    window.put(s.charAt(start),window.get(s.charAt(start))-1);
                }
                start++;
                flag=true;//说明出现了一个新的符合要求的子串
                flag2=true;//如果进了这个循环，说明至少存在一个满足条件的子串
            }
            if(flag&&(end-start+1<len)){
                len=end-start+1;
                fstart=start-1;
                fend=end-1;
            }
        }
        if(fend==fstart&&!flag2){
            return re;//不存在满足要求的子串就返回""
        }
        else{
            return s.substring(fstart,fend+1);
        }
    }
    boolean flag2map(HashMap<Character,Integer> need,HashMap<Character,Integer> window){
        for(Character tmp: need.keySet()){
            Integer win=window.get(tmp);
            if(win==null)return false;//不存在对应key也返回false
            if(need.get(tmp).intValue()>win.intValue())return false;//这里注意是大于号，window中字符出现次数小于need中对应次数就返回false
            //注意integer要转成int来比较大小
        }
        return true;
    }
}

字符串排列

题目#567

给定两个字符串 s1 和 s2，写一个函数来判断 s2 是否包含 s1 的排列。

换句话说，第一个字符串的排列之一是第二个字符串的子串。

示例1:

输入: s1 = “ab” s2 = “eidbaooo”
输出: True
解释: s2 包含 s1 的排列之一 (“ba”).

示例2:

输入: s1= “ab” s2 = “eidboaoo”
输出: False

思路:维护一个s1长度的窗口，不是排列就right+1，left+1，即向右平移窗口。

class Solution {
    public boolean checkInclusion(String s1, String s2) {
        HashMap<Character,Integer> need=new HashMap<>();
        HashMap<Character,Integer> window=new HashMap<>();
        //记录s1每个字符出现次数
        for(int i=0;i<s1.length();i++){
            need.put(s1.charAt(i),need.getOrDefault(s1.charAt(i),0)+1);
        }
        int left=0,right=s1.length()-1;//窗口大小就是s1长度
        if(right>=s2.length())return false;
        for(int i=0;i<=right;i++){//记录窗口中每个字符出现次数
            window.put(s2.charAt(i),window.getOrDefault(s2.charAt(i),0)+1);
        }       
        while(true){
            if(check(need,window))return true;
            //平移窗口
            left++;
            right++;
            if(right>=s2.length())break;
            window.put(s2.charAt(right),window.getOrDefault(s2.charAt(right),0)+1);
            window.put(s2.charAt(left-1),window.getOrDefault(s2.charAt(left-1),0)-1);
        }
        return false;
    }
    boolean check(HashMap<Character,Integer> need,HashMap<Character,Integer> window){
        for(Character tmp: need.keySet()){
            if(need.get(tmp).intValue()!=window.getOrDefault(tmp,-1).intValue())return false;
        }
        return true;
    }
}

找到字符串中所有字母异位词

题目：#438

给定一个字符串 s 和一个非空字符串 p，找到 s 中所有是 p 的字母异位词的子串，返回这些子串的起始索引。

字符串只包含小写英文字母，并且字符串 s 和 p 的长度都不超过 20100。

说明：

字母异位词指字母相同，但排列不同的字符串。
不考虑答案输出的顺序。
示例 1:

输入:
s: “cbaebabacd” p: “abc”

输出:
[0, 6]

解释:
起始索引等于 0 的子串是 “cba”, 它是 “abc” 的字母异位词。
起始索引等于 6 的子串是 “bac”, 它是 “abc” 的字母异位词。

思路和上面一样

class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        HashMap<Character,Integer> need=new HashMap<>();
        HashMap<Character,Integer> window=new HashMap<>();
        List<Integer> re=new LinkedList<>();
        //记录s1每个字符出现次数
        for(int i=0;i<p.length();i++){
            need.put(p.charAt(i),need.getOrDefault(p.charAt(i),0)+1);
        }
        int left=0,right=p.length()-1;//窗口大小就是s1长度
        if(right>=s.length())return re;
        for(int i=0;i<=right;i++){//记录窗口中每个字符出现次数
            window.put(s.charAt(i),window.getOrDefault(s.charAt(i),0)+1);
        }       
        while(true){
            if(check(need,window))re.add(left);
            //平移窗口
            left++;
            right++;
            if(right>=s.length())break;
            window.put(s.charAt(right),window.getOrDefault(s.charAt(right),0)+1);
            window.put(s.charAt(left-1),window.getOrDefault(s.charAt(left-1),0)-1);
        }
        return re;
    }
    boolean check(HashMap<Character,Integer> need,HashMap<Character,Integer> window){
        for(Character tmp: need.keySet()){
            if(need.get(tmp).intValue()!=window.getOrDefault(tmp,-1).intValue())return false;
        }
        return true;
    }
}

最长无重复子串

题目：#3

给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。

示例 1:

输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。
示例 2:

输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。
示例 3:

输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是子串的长度，”pwke” 是一个子序列，不是子串。

import java.util.*;
class Solution {
    public int lengthOfLongestSubstring(String s) {
        HashMap<Character,Integer> window=new HashMap<>();
        int left=0,right=0;
        int maxlen=0;
        while(right<s.length()){
            while(right<s.length()&&(window.getOrDefault(s.charAt(right),0)==0)){//右移扩大窗口直到出现重复字符或越界
                window.put(s.charAt(right),1);//将字符加入窗口中
                right++;           
            }
            maxlen=Math.max(maxlen,right-left);//更新最大长度
            if(right==s.length())break;
            while(window.getOrDefault(s.charAt(right),0)!=0){//右移缩小窗口直到窗口中无重复字符
                window.put(s.charAt(left),0);
                left++;
            }
        }
        return maxlen;
    }
}

双指针

快慢指针

判断链表是否有环（有环两个指针最终会相遇）
找链表中点（快指针到链表末端，慢指针到中点）
寻找链表倒数第k个数（快指针先走k步，再和慢指针一起同速走）

左右指针

二分查找
有序数组中找两个数之和为目标值（左指针为0，右指针为末尾，两数和小于目标值，left++，大于，right–）
反转数组
滑动窗口

BFS

本质是图中找最短路径

核心数据结构是队列

框架

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    Queue<Node> q; // 核心数据结构
    Set<Node> visited; // 避免走回头路

    q.offer(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数

    while (q not empty) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) {
            Node cur = q.poll();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj())
                if (x not in visited) {
                    q.offer(x);
                    visited.add(x);
                }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

例题

打开转盘锁

题目#752

你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字： ‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’ 。每个拨轮可以自由旋转：例如把 ‘9’ 变为 ‘0’，’0’ 变为 ‘9’ 。每次旋转都只能旋转一个拨轮的一位数字。

锁的初始数字为 ‘0000’ ，一个代表四个拨轮的数字的字符串。

列表 deadends 包含了一组死亡数字，一旦拨轮的数字和列表里的任何一个元素相同，这个锁将会被永久锁定，无法再被旋转。

字符串 target 代表可以解锁的数字，你需要给出最小的旋转次数，如果无论如何不能解锁，返回 -1。

思路：

对于每次数字，都有8个相邻选择（4位，每位+1或-1），每次把这些选择入队
用一个set记录访问过的数字组合
String和char数组的转换：s.toCharArray() ,new String(ch)
int和char转换：(char)(num+'0'),ch-'0'

class Solution {
    public int openLock(String[] deadends, String target) {
        Queue<String> que=new LinkedList<>();
        Set<String> visited=new HashSet<>();
        for(String dead:deadends){
            visited.add(dead);
        }
        if(visited.contains("0000"))return -1;
        que.offer("0000");
        visited.add("0000");
        int size=0;
        int num=0;
        String tmp;
        while(!que.isEmpty()){
            size=que.size();
            for(int i=0;i<size;i++){
                tmp=que.poll();
                if(tmp.equals(target))return num;               
                for(int j=0;j<4;j++){
                    String tmp2=plusUp(tmp,j);
                    if(!visited.contains(tmp2)){
                        que.offer(tmp2);
                        visited.add(tmp2);//入队的时候加入visited会耗时更少，出队才加会超时
                    }
                    String tmp3=plusDown(tmp,j);
                    if(!visited.contains(tmp3)){
                        que.offer(tmp3);
                        visited.add(tmp3);
                    }
                }
            }
            num++;
        }
        return -1;
    }
    String plusUp(String str,int i){
        char [] ch=str.toCharArray();
        ch[i]=(char)('0'+((ch[i]-'0')+1)%10);
        return new String(ch);
    }
    String plusDown(String str,int i){
        char [] ch=str.toCharArray();
        ch[i]=(char)('0'+((ch[i]-'0')+9)%10);
        return new String(ch);
    }
}

回溯

适合做排列组合问题，即遍历所有可行解。

框架

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

路径的数据结构：用Stack或者Deque，后者效率更高

Deque<Integer> path=new LinkedList<>();
path.addLast(x);
dfs();
path.removeLast();

//如果返回类型是List，可以直接queue转List
LinkedList<Integer> tmp=new LinkedList<>(path);

选择列表：

特别注意确定选择列表到底是什么

例如：

子集问题#78，选择列表是当前数是否选，二选一
组合总和问题#39，选择列表是所有可选的数，n选一

去重：

不讲顺序（1,2,3和2,1,3认为是一样的）：使用begin标记选择列表的开始，每次从begin开始往后遍历
讲顺序，用数组

例题

子集

题目：#78

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

思路：

不讲顺序，用begin，选择列表是当前数选或者不选

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> re=new LinkedList<>();
        Deque<Integer> path=new ArrayDeque<>();
        dfs(nums,re,path,0);
        return re;
    }
        private void dfs(int[] nums,List<List<Integer>> re,Deque<Integer> path,int begin){
        if(begin==nums.length){
            ArrayList<Integer> tmp=new ArrayList<>(path);
            re.add(tmp);
            return;
        }
        //当前数不选
        dfs(nums,re,path,begin+1);
        //当前数选
        path.addLast(nums[begin]);
        dfs(nums,re,path,begin+1);
        path.removeLast();
    }
}

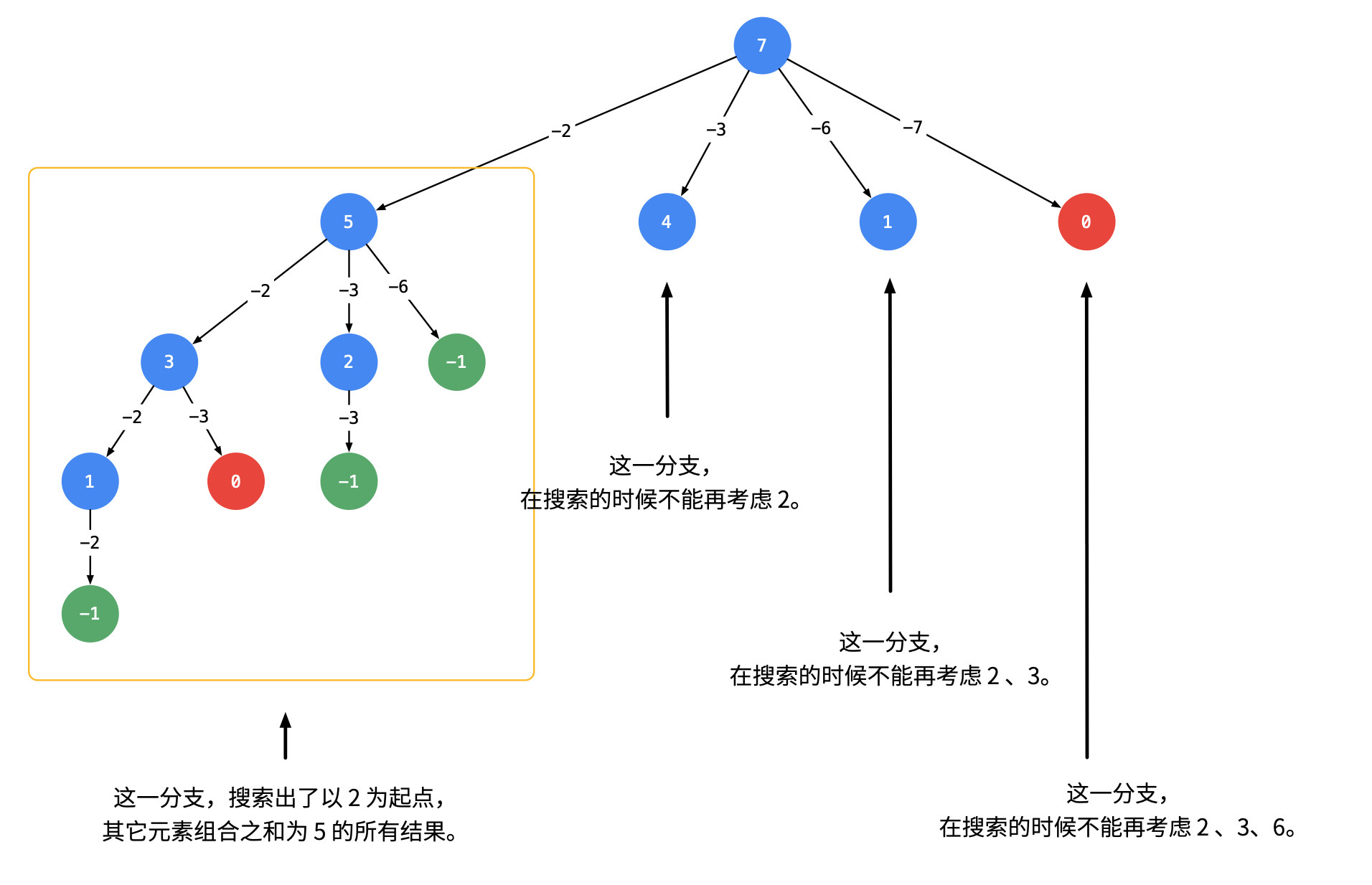
组合总和

题目：#39

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。

说明：所有数字（包括 target）都是正整数。解集不能包含重复的组合。

思路：

不讲顺序，用begin,选择列表是candidates里的所有数，n选1

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> re=new LinkedList<List<Integer>>();
        if(candidates.length==0)return re;
        Arrays.sort(candidates);
        Deque<Integer> path=new ArrayDeque<>();
        dfs(candidates,target,re,path,0);
        return re;
    }
    void dfs(int[] candidates, int target,List<List<Integer>> re,Deque<Integer> path,int begin){
        if(target==0){
            re.add(new ArrayList<>(path));
            return;
        }
        for(int i=begin;i<candidates.length;i++){//选择列表n选1
            if(candidates[i]>target){
                break;
            }
            else{
                path.offerLast(candidates[i]);
                dfs(candidates,target-candidates[i],re,path,i);
                path.pollLast();
            }
        }
    }
}

单词搜索

题目：#79

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:

board =
[
[‘A’,’B’,’C’,’E’],
[‘S’,’F’,’C’,’S’],
[‘A’,’D’,’E’,’E’]
]

给定 word = “ABCCED”, 返回 true
给定 word = “SEE”, 返回 true
给定 word = “ABCB”, 返回 false

思路：

这个是讲顺序的，所以要用一个visited数组来记录访问过的数

class Solution {
    public boolean exist(char[][] board, String word) {
        int row=board.length;
        int col=board[0].length;
        boolean[][]visited=new boolean[row][col];
        for (int i = 0; i <row ; i++) {
            for (int j = 0; j < col; j++) {
                if(starExist(board,word,i,j,0,visited))return true;
            }
        }
        return false;
    }
    boolean starExist(char[][] board, String word,int i,int j,int idx,boolean[][]visited){
        
        if(i<0||i>=board.length||j<0||j>=board[0].length)return false;
        if(visited[i][j])return false;   
        if (board[i][j]==word.charAt(idx)){
            if(idx==word.length()-1)return true;
            visited[i][j]=true;
            //注意这里如果是true就要直接返回，不然会多做无用的递归超时
            if(starExist(board,word,i-1,j,idx+1,visited))return true;
            if(starExist(board,word,i+1,j,idx+1,visited))return true;
            if(starExist(board,word,i,j-1,idx+1,visited))return true;
            if(starExist(board,word,i,j+1,idx+1,visited))return true;
            visited[i][j]=false;
            return false;
        }
        else{
            return false;
        }
    }
}

并查集

并查集是一种树型的数据结构，用于处理一些不交集的合并及查询问题。它可以支持两种操作

(1) 将两个不相交的集合合并

(2) 判断两个元素是否在一个集合中

两种操作的时间复杂度近乎O ( 1 )

框架

用一个数组p来存储每个节点的父节点的编号，即 p [ x ] 表示编号为 x 的结点的父节点的编号为 p [ x ]

初始化：把每个点所在集合初始化为自己，即p [ x ] = x

查找：

int find(int x){
 if(p[x] != x) p[x] = find(p[x]);
 return p[x];
}

合并：

1
2
3

void union(int[] p, int a, int b){
 p[find(a)] = find(b); //a的祖宗结点find(a) 作为 b的祖宗结点find(b)的子节点
}

例题

无向图中连通分量的数目

题目：323

class Solution {
    int[] parent;//这是记录关系的数组

    //查找
    int find(int parent[], int i) {
        if (parent[i] == -1)
            return i;
        return find(parent, parent[i]);
    }

    //合并
    void union(int parent[], int x, int y) {
        int xset = find(parent, x);
        int yset = find(parent, y);
        if (xset != yset)
            parent[xset] = yset;
    }

    public int countComponents(int n, int[][] edges) {
        int len = edges.length;
        parent = new int[n];
        Arrays.fill(parent, -1);
        for (int i = 0; i < len; i++) {
            union(parent, edges[i][0], edges[i][1]);
        }
        int count = 0;
//查根的数量
        for (int i = 0; i < n; i++)
            if (parent[i] == -1)
                count++;
        return count;
    }
}